Laatst las ik in het FD (het financieele dagblad) een artikel van Erica Verdegaal, de titel was “Wees toch geen kuddedier in geldzaken”. In dit artikel werden een aantal voorbeelden weergegeven waarin werd aangetoond dat onze beslissingen niet altijd rationeel zijn uit te leggen.
Een voorbeeld gaat over de macht van de grote getallen (bigness bias). Vrijwel iedereen heeft de neiging grote getallen belangrijker te vinden dan de kleine. Wij als financieel planners weten dat juist kleine getallen over een lange periode het verschil maken! Ik zal u dat proberen uit te leggen aan de hand van een paar voorbeelden.
De tweelingbroers Tom en Aad
Beiden willen zij geld voor later opzij zetten, Tom stort van zijn 20ste tot zijn 35ste (dus 15 jaar lang) elke maand € 100 in een beleggingsfonds. Vervolgens laat hij deze inleg vanaf zijn 35ste tot zijn 70ste doorgroeien. Hij stort niets meer bij.
Zijn broer Aad pakt het anders aan. Hij belegt tot zijn 35ste helemaal niets, hij begint dan pas. Vanaf zijn 35ste tot zijn 70ste, dus 35 jaar lang stort Aad maandelijks € 100 in hetzelfde beleggingsfonds als Tom.
Stel nu dat het beleggingsfonds gemiddeld 5% rendement per jaar maakt. Wie is er dan op zijn 70ste het rijkst?
Dat is Tom, hoewel hij in totaal slechts € 18.000 heeft gestort en Aad € 42.000. Toch bezit Tom op zijn 70ste dan € 141.155, terwijl Aad ‘maar’ € 111.298 heeft.
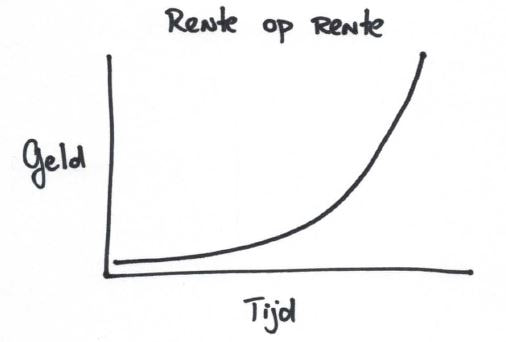
Het is niet raar als u dit anders had ingeschat. Vrijwel iedereen heeft de neiging grote aantallen (35 jaar, € 42.000) belangrijker te vinden dan kleine (15 jaar, € 18.000). Reken dus nooit op gevoel, maar met een rekenprogramma. Op internet zijn handige tools te vinden, zelf gebruik ik www.berekenhet.nl regelmatig. Daar komt ook onderstaande grafiek vandaan.
Deze grafiek geeft weer wat de vermogensopbouw is van iemand, laten we haar Inge noemen, die op 30-jarige leeftijd maandelijks € 200 in een beleggingsfonds stort (gemiddeld 5% rendement). Na 35 jaar heeft Inge een bedrag van € 222.596 bij elkaar belegd. Stel dat Inge 2 jaar later begint dan zou ze op € 197.318 zijn uitgekomen. Wanneer zij 10 jaar later zou zijn begonnen, dan zou ze blijven steken op € 117.624.
Stel nu dat Inge op 65-jarige leeftijd daadwerkelijk die € 222.596 nodig heeft, bijvoorbeeld om haar aflossingsvrije hypotheek af te lossen of pensioenaanvulling. Maar ze begint pas 10 jaar later, dan zou ze gedurende 25 jaar € 370 per maand moeten beleggen.
Wat de inleg betreft een behoorlijk verschil, € 84.000 (420 keer € 200) tegenover € 111.000 (300 keer € 370).